Szybkie obliczenia w grafach planarnych (klastry)¶
grafy planarne: można narysować na płaszczyźnie bez przecinających się krawędzi;
mają ciekawe właściwości...
- można "ścisnąć" kraw i znów otrzymamy graf planarny (tzn minor)
- istnieje 4-kolorowanie-wierz
oraz wiele innych cech przydatnych algorytmicznie...
chcemy obliczać -aproksymację problemów:
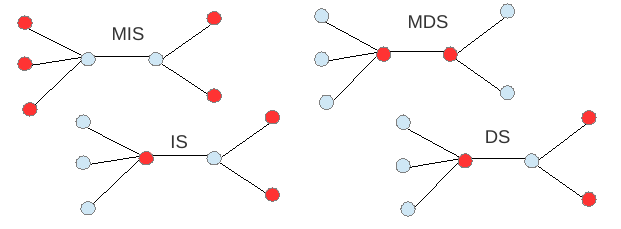
- MM (Maximum Matching),
- MDS (Minimum Dominating Set),
- MIS (Maximum Independent Set);
def tych problemów, patrz:
def -aproksymacji dla problemów typu maximum:
- rozw produkowane przez algorytm,
- rozw optymalne,
Koncepcja "klastrów" ...¶
czy warto centralizować obliczenia, tzn
- sciągnąć cały graf do centrum obliczeniowego,
- rozwiązać problem na 1 wierz,
- rozesłać rozwiązanie po całym grafie

Jest probelm: pkt 1. i 3. są bardzo czasochłonne jeśli graf ma dużą średnicę...
Rozwiązanie: klastry o małej średnicy i małym brzegu...
w każdym klastrze, równolegle i niezależnie, wykonujemy pkt 1. 2. 3.
dlaczego brzeg ma być "mały" ? aby błąd na brzegu też był mały !!
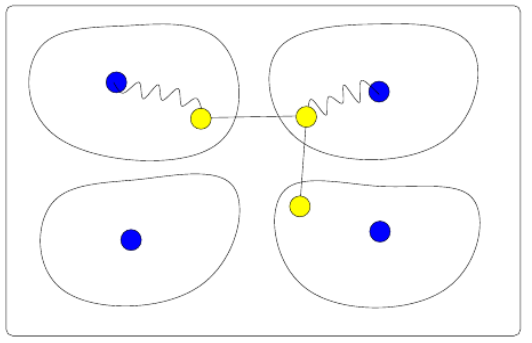
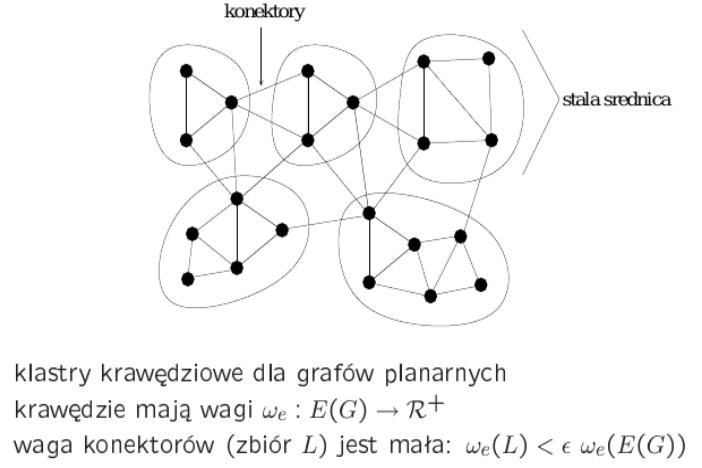
def klastrów:
klastry to podział zbioru wierz na podzbiory ,
taki, że podgraf indukowany jest spójny i ma małą (stałą) średnicę;
ponadto konektory (krawędzie miedzy klastrami), muszą mieć małą łączną wagę;
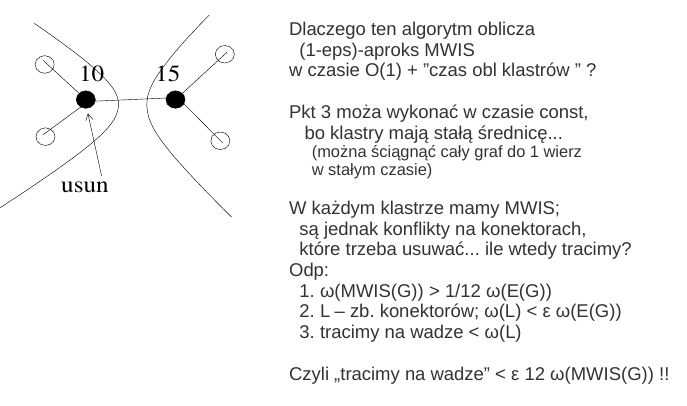
Mamy klastry, to jak obliczyć -aproks MWIS ?¶
MWIS to ważona wersja problemu MIS (wagi na wierz);

Dlaczego powyższe obliczenia dają nam -aproks MWIS ???
odp:
Mamy klastry, to jak obliczyć -aproks MM ?¶
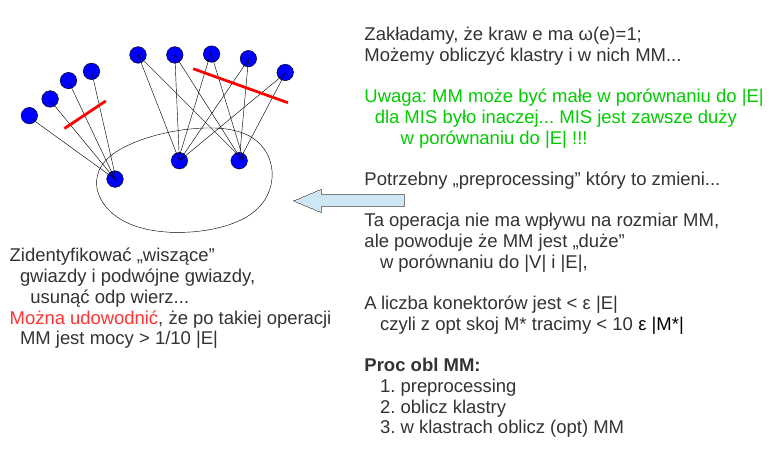
Mamy klastry, to jak obliczyć -aproks MDS ?¶
To jest najtrudniejszy z tych problemów...
Wydaje się że nie powinno być żadnego problemu:
- obl klastry,
- w klastrach obl MDS (nie ma konfliktów na konektorach jak w MIS!),
- rozsyłamy rozw po klastrze,
Dlaczego takie podejście nie dziala ???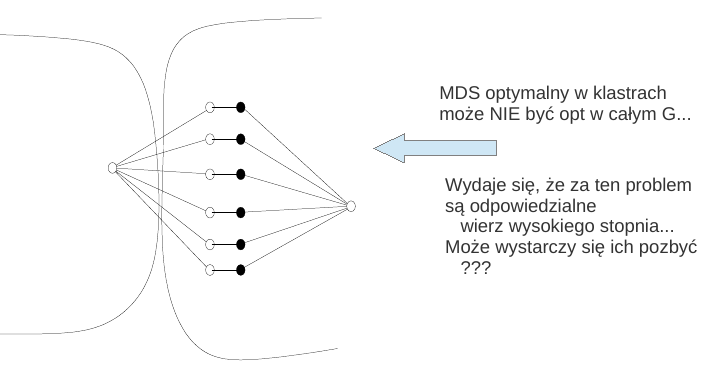
Próba rozwiązania problemu jak w MM - nieskuteczna...
Problem stanowią wierz wysokiego stopnia, jak się ich pozbyć ?
zapewne znowu „preprocesing” (tak jak było w przypadku MM);
jaki preprocessing ? np. taki:
włączyć do rozw wszystkie wierz wysokiego stopnia i usunąć zdominowane wierz,
pozostanie graf BEZ wierz wysokiego stopnia...
TO NIE DZIAŁA !!!
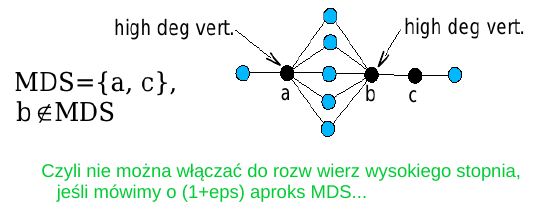
Zatem jak rozwiązać problem dla MDS ???
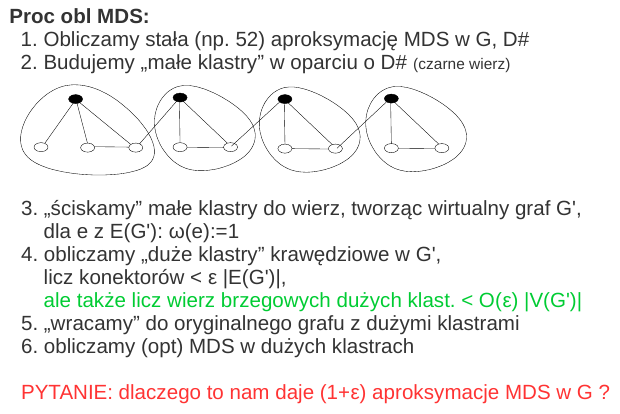
... i odpowiedź na powyższe pytanie:
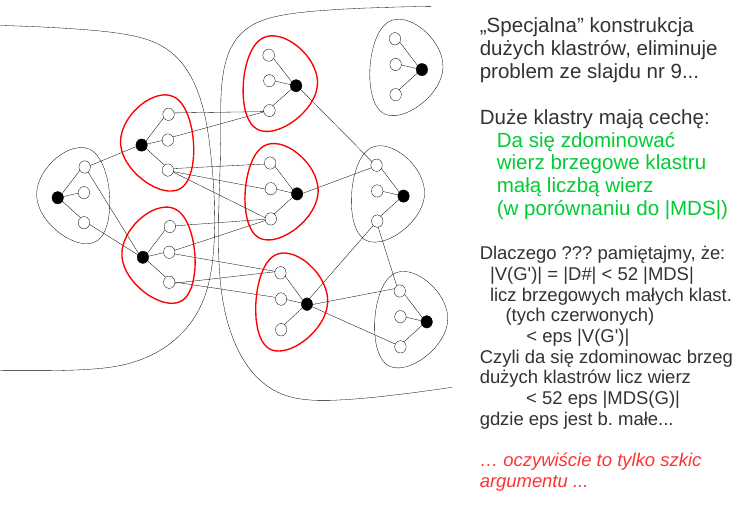
Uwaga: jeśli wagi kraw =1, to nie tylko liczba konektorów jest mała,
ale także liczba wierz brzegowych (końców konektorów) jest mała,
w grafie planarnym...
Jak obliczamy klastry w grafie planarnym ?¶
Tu jest opisana procedura obliczająca klastry w czasie

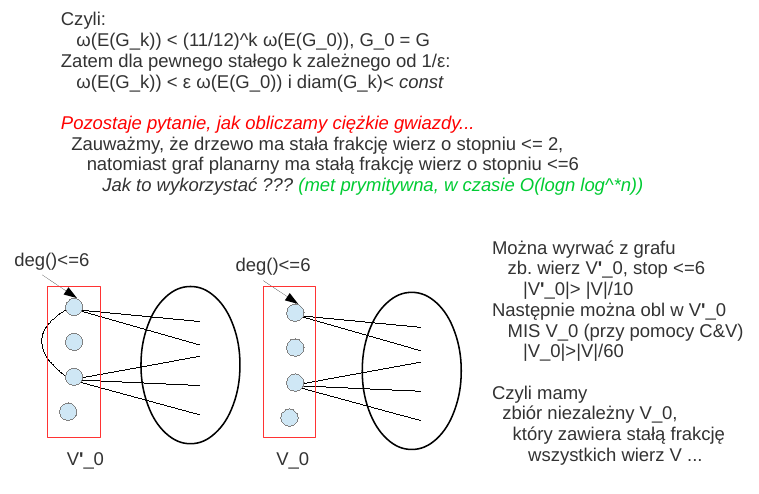
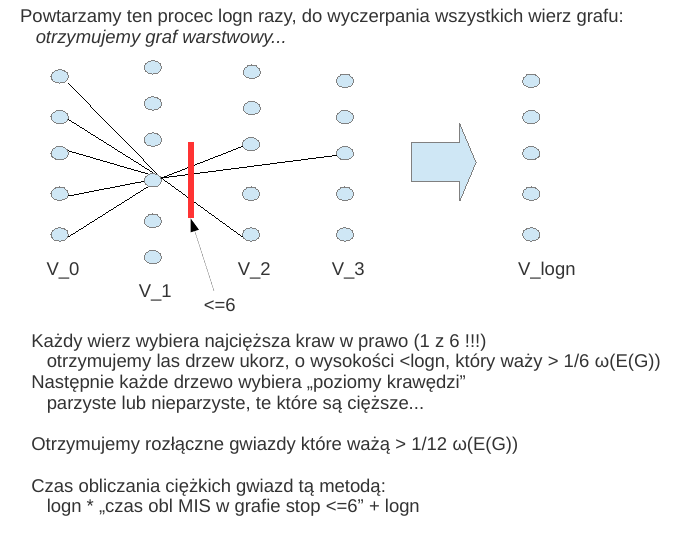
Uwaga: isnieje szybsza procedura obl klastów w czasie
Jaka jest wada metody klastrów ?
odp: długie komunikaty, np. przy ściaganiu obrazu grafu do centrum...
...
Zadania¶
ZADANIE 60 ciężkie gwiazdy w drzewie ukorzenionym
Dane jest drzewo ukorzenione , z wagami na krawędziach.
Zaimplementuj algorytm synch znajdujący rozłączne gwiazdy o ŁĄCZNEJ wadze .
Czas działania algorytmu powinien być rzędu .
Uwaga: nie należy używać długich komunikatów, tj nie zbierać obrazu całego drzewa w korzeniu!
Zakładamy, że wierz znają wysokość(T).
ZADANIE 61 orientacja kraw z outdeg<=2 w drzewie
Zaimplementuj algorytm znajdujący orientację krawędzi z outdeg<=2 w drzewie nieukorzenionym!
ZADANIE 62 (2pkt) szybka orientacja kraw z outdeg<=2 w drzewie
Jak poprzednie, ale czas działania ograniczony przez lub lepszy.
ZADANIE 63 ściąganie info o grafie do każdego wierz
Napis algorytm dla grafu kratowego, x wierz,
w którym każdy wierz poznaje zbiór ID (id_los) wszystkich wierz;
staraj się unikać zbyt długich komunikatów!!
ZADANIE 64 (4pkt) (prj+ref) szybkie ciężkie gwiazdy w drzewie
Obliczać szybko "ciężkie gwiazdy" w drzewie.
Czas działania ograniczony przez .