skojarzenia w modelu rozproszonym...¶

skojarzenie (matching) maximum, maximal, wsp aproksymacji:

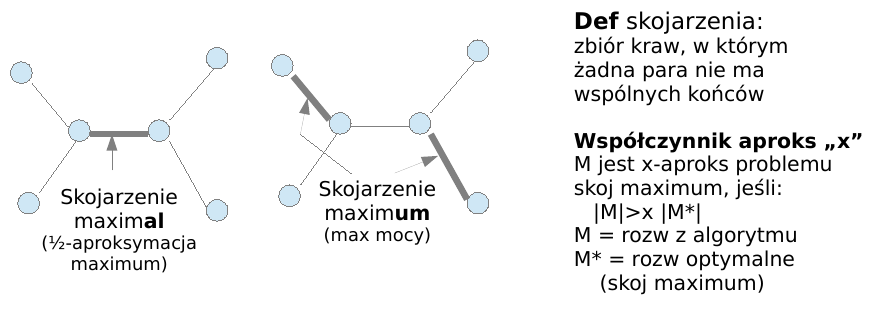
zajmiemy się obliczaniem skojarzeń głównie w grafach dwudzielnych; motywacja ???
wszystkie alg są synch i deterministyczne, działają w czasie polylog(n)

istnieje kilka algorytmów:

1. "stary" (1999) algorytm obliczający skoj maximal w czasie O(log^4n)
   używa struktur danych: D-bloków, spannerów, oraz "dzielenia stopnia przez 2", patrz tutaj
2. "nowy" algorytm (M. Fischer 2017), skoj maximal w czasie O(log^3n), a stała aproks w czasie O(log^2n)
   używa rozwiązania frakcyjnego, które potem jest zaokrąglane

oba algorytmy używają procedury dzielenia cyklu/ścieżki na zorientowane segmenty ... (patrz ZADANIE ??)

stary algorytm (tylko szkic...)¶

naszkicujemy, jak obliczas sie skoj w grafie dwudzielnym...

1. redukcja do D-bloków, grafów z prawie równym stopniem po lewej
2. "dzielenie stopni przez 2" w D-blokach, aż uzyskamy spanner
   (gwiazdy z ograniczonym stopniem po prawej, przykrywające 50% wierz z lewej)
3. spanner zamieniamy na dobre skojarzenie (dokładnie: koszące)
   skoj koszące to takie, w którym stały % kraw jest do niego incydentny

graf dwudzielny -> D-bloki:

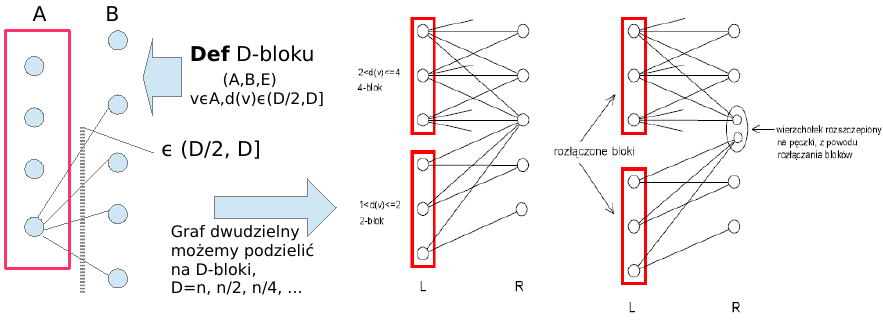
dla każdego D-bloku, rozbijamy wierz na pęczki i logD razy "dzielimy przez 2":

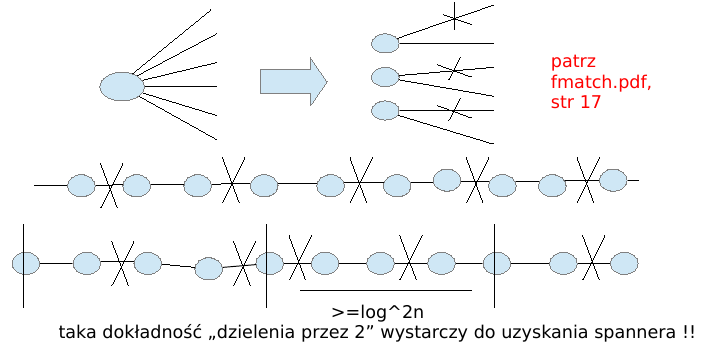
otrzymujemy spanner, który zawiera skoj koszące...

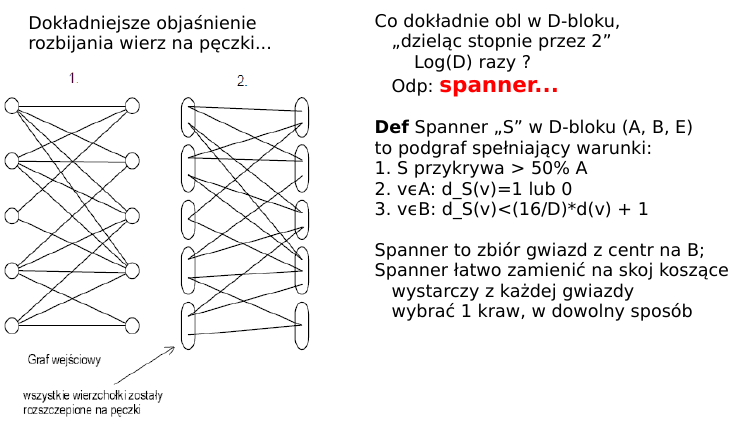
mając skoj koszące w grafie, usuwamy "skojarzone" wierz, powtarzamy logn razy...

Uwaga 1: widać, że kluczową rolę odgrywa "dzielenie stopni przez 2",
co wymaga wybrania co 2 kraw w cyklach/ ścieżkach (2-kol-kraw cyklu/ ścieżki), wiemy, że to nie jest łatwe, ale na szczęście nie trzeba tego robić dokładnie...

Uwaga 2: ten sam mechanizm przybliżonego 2-kol-kraw jest używany przez alg M. Fischer!!

nowy algorytm (M. Fischer, 2017)¶

zaczynamy od rozwiązania frakcyjnego, czyli liczby z [0,1] zamiast z {0,1} na kraw...
wymagania co do rozw frakcyjnego takie jak dla zwykłego skoj...

teraz musimy "zaokrąglić" liczby z [0,1] do {0,1},
nie tracąc na wadze, i nie psując warunków wierz...

jakie wartości przyjmują liczby Xe ? odp: {2^0/Delta, 2^1/Delta, 2^2/Delta, …, 2^(log Delta)/Delta}
na początku patrzymy TYLKO na kraw z Xe=2^i/Delta, i=0
wierz rozbiamy na pęczki stopnia 2 i ew. jeden stopnia 1...

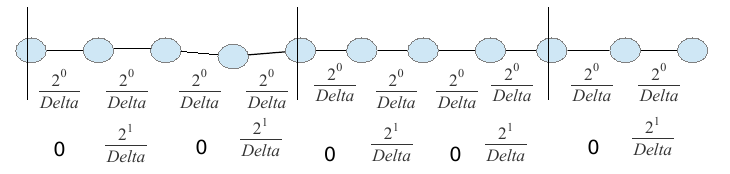
wyeliminowaliśmy kraw z Xe=2^0/Delta, ale łączna waga się nie zmieniła!!
w ten sam sposób eliminujemy kraw z Xe=2^1/Delta, Xe=2^2/Delta, …
zostają kraw z Xe=0 i Xe=1, suma Xe jest w przybl taka jak na początku! warunki wierz też ok!
ZATEM mamy prawdziwe skoj (stałą aproks)...
z obliczeń wynika, że segmenty muszą mieć długość >=logn (a nie >=log^2n)

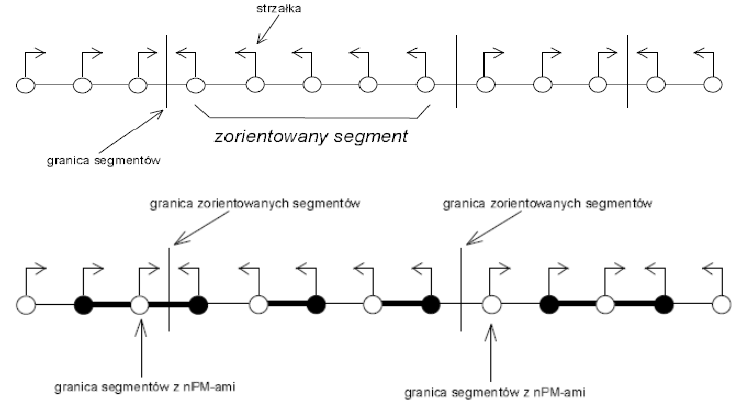
procedura dzielenia cyklu/ścieżki na zorientowane segmenty¶

celem jest podzielenie cyklu/ścieżki na zorientowane segmenty...
alg podziału na segm o dł>=L powinien działać w czasie O(L)
co to ma wspólnego z 2-kol-kraw ? odp: zorient segmenty + 2-kol-wierz = 2-kol-kraw w segmentach !!
im dłuższe segmenty tym mniej "granic" (= przekłamań) 2-kol-kraw
także: tym dokładniejsze "dzielenie stop przez 2" lub "zaokrąglanie"...

Zadania¶

ZADANIE 30 alg M. Fischer/ rozwiązanie frakcyjne
zaprogramuj algortym synch obliczający rozwiązanie frakcyjne skojarzenia

ZADANIE 31 (3pkt) (prj+ref) obliczanie zorient segm o dł>L w czasie O(L)
jest to procedura, która w połączeniu z 2-kol-wierz "na wejściu"
pozwalająca uzyskać 2-kol-kraw w segm o dł>L w czasie O(L), L=logn (nowy alg) lub L=log^2n (stary alg)

ZADANIE 32 skoj maximal w grafie dwudzielnym, (L,R,E), o stałym Delta(L)
alg powinien działać w stałym czasie zależnym od Delta(L) (max stopien na zbiorze L);
wskazówka: proponowanie kraw z lewej i usuwanie nadmiarowych propozycji z prawej;
dlaczego to działa w stałym czasie??