Proste i zaawansowane alg wyboru lidera w cyklu (LE = Leader Election).¶

LE, asynch, cykl zorientowany, liczba komunikatów O(n^2)¶

LE w cyklu n^2
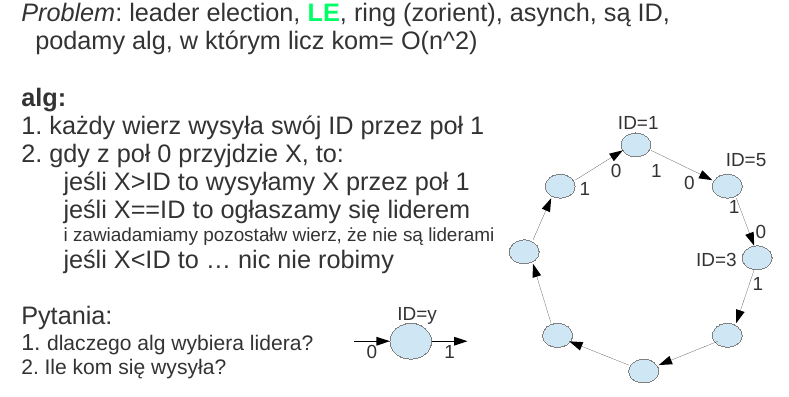
jedynie max ID wykonuje pełne koło, inne komunikaty są "połykane" po drodze...
dlaczego wysyła się (pesymistycznie) O(n^2) komunikatów ? odp:
LE w cyklu n^2 c.d.

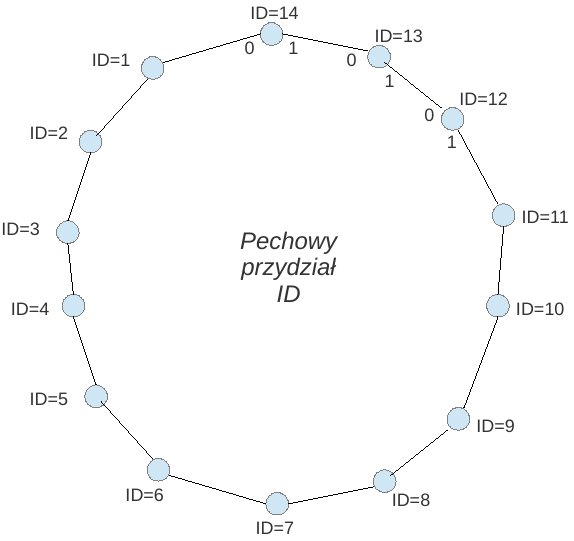
poniżej (niepełna) implementacja powyższego algorytmu:

## LE, O(n^2) kom, symulator synch (choć alg jest asynch!)
# + nie ma tu zawiadamiania nie-liderow, że nie są liderami;
#   proszę samodzielnie uzupełnić ten brak...
#
import tkinter; t=tkinter.Tcl()
t.eval("""
source symul_lib.tcl; # ladowanie symulatora

set liczbaWierz 10
iterate i $liczbaWierz {
  let i1 $i-1; if {$i1==-1} {let i1 $liczbaWierz-1}
  let i2 $i+1; if {$i2==$liczbaWierz} {let i2 0}
  set sasiedzi($i) "$i1 $i2"
}

fiber create $liczbaWierz run

fiber_iterate {
proc run {} {
  global lider id_los run kom

  set lider ?

  wyslij 1 $id_los
  fiber yield

  while {$run} {
    if {$kom(0)!=""} {
      #set x $kom(0)
      #set x [lindex $kom(0) 0]
      set x [czytaj 0]
      if {$x > $id_los} {
         wyslij 1 $x
      } elseif {$x == $id_los} {
         set lider 1
      }
    }
    fiber yield
  }
}
}

Inicjalizacja; # koniecznie trzeba to wywolac!!!
proc _puts s {global _; append _ "$s\n"}; # specjalnie dla jupyter-a...

set liczRund 0
proc wizualizacja {} {
  _puts "---[incr ::liczRund]---"
  fiber_iterate {_puts "$id, $id_los, $lider: $kom(0), $kom(1)"}
  global licznikKom
  _puts "liczba kom=$licznikKom"
}

""")

''

# uruchomienie pojedynczej rundy...
print(t.eval("""
set _ ""; # można zakomentować...
fiber yield; runda; wizualizacja; set _
"""))

---11---
0, 885, ?: , 
1, 157, ?: , 
2, 584, ?: , 
3, 578, ?: , 
4, 805, ?: , 
5, 988, 1: , 
6, 260, ?: , 
7, 39, ?: , 
8, 56, ?: , 
9, 602, ?: , 
liczba kom=26

# restartowanie symulacji...
print(t.eval("""
set_run 0; fiber yield; 
set_run 1; fiber restart; set licznikKom 0
"""))

0

# wyswietla opisy błędów w fiberach...
print(t.eval('fiber error'))

{} {} {} {} {} {} {} {} {} {}

Zadania¶

Uwaga: zadania można robić bezp w jupyterze LUB zewn symulatorem (w konsoli2c)

ZADANIE 10 "LE, cykl NIE-zorientowany"
Do powyższego alg "LE, asynch, O(n^2) kom" dodaj możliwość pracy w cyklu NIE-zorientowanym;
niech NIE-liderzy wiedzą, że nie są liderami;
użyj symulatora synch;

ZADANIE 11 "LE, 2 liderów w cyklu"
Zmodyfikuj alg "LE, asynch, O(n^2) kom" w cyklu zorientowanym aby wybierał 2 liderów;
niech NIE-liderzy wiedzą, że nie są liderami;
użyj symulatora synch;

LE, asynch, cykl, są ID, liczba komunikatów O(n logn)¶

LE, O(n logn)

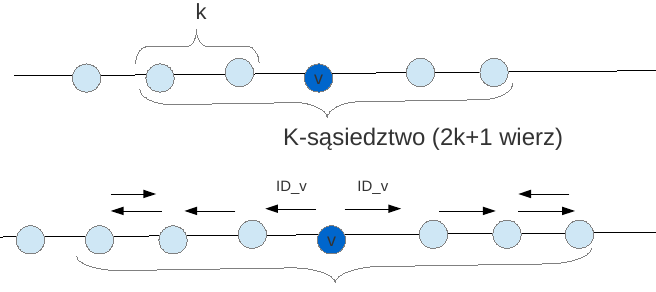
Algorytm używa pojęcia k-sąsiedztwa i działa w fazach...
mamy fazy: 0, 1, 2, …
wierz uczestniczące w L-tej fazie wykonują pewną operację w 2^L- sąsiedztwie
wierz v wysyła ID_v w obie strony + zasady "połykania" kom, jak z LE O(n^2)
jeśli wierz otrzyma odpowiedź z obu stron to ogłasza się „tymczasowym liderem L-tej fazy”
w fazie L+1 uczestniczą tymczasowi liderzy L-tej fazy

Kluczowy lemat: LE, O(n logn), lemat

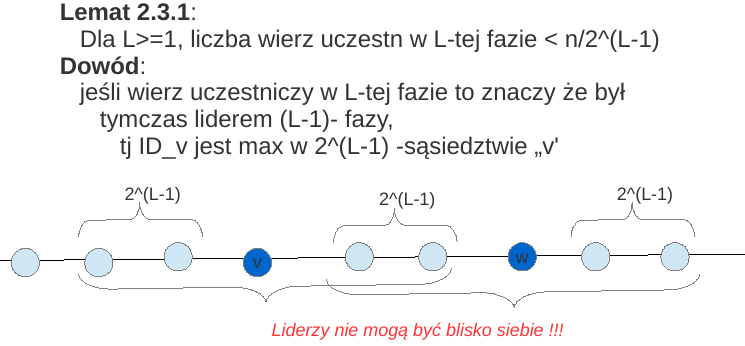
Skoro każdy wierz uczestniczący w fazie L wysyła 4 2^L kom,
to w L-tej fazie łącznie wysyła się 4 2^L n/2^(L-1) = 8n kom.
Liczba faz wynosi logn (dlaczego ??) stąd złożoność komunikatowa algortymu to O(n logn) ...

LE, synch, cykl, są ID, non-uniform (zna "n"), liczba komunikatów O(n)¶

LE, synch, non-uniform

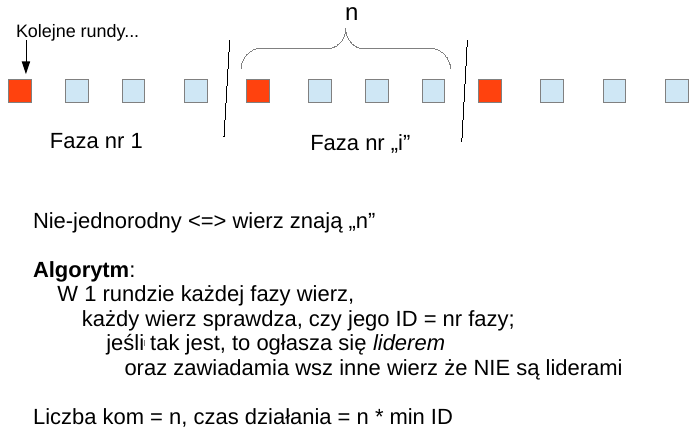
LE, synch, cykl, są ID, uniform, liczba komunikatów O(n)¶

LE, synch, uniform
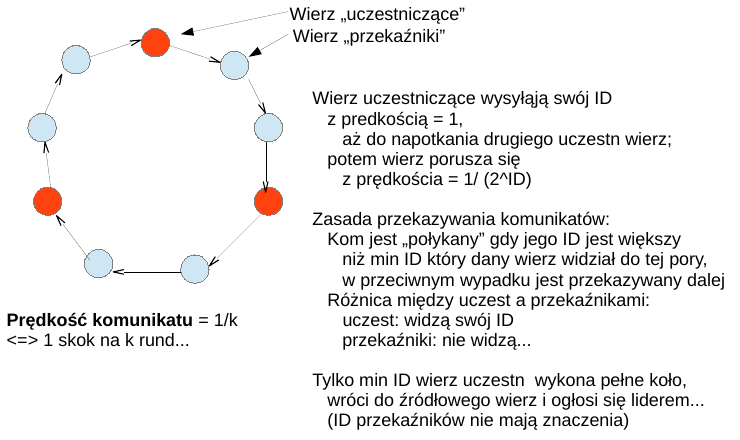
Jaka intuicja kryje się za tym alg? odp:
liderem jest wierz z min ID, ten wierz porusza się najszybciej;
wierz z większym ID poruszają się wolniej, zatem mniej niepotrzebnych kom sie wysyła!

Analiza algorytmu:
LE, synch, uniform

Zadania¶

ZADANIE 12 (3pkt) "LE, asynch, cykl, O(n logn) kom"
Zaimplementuj powyższy algorytm;
użyj symulatora synch;

ZADANIE 13 "LE, synch, cykl, non-uniform, O(n) kom"
Zaimplementuj powyższy algorytm;
użyj symulatora synch (nic dziwnego);
id_los powinny być losową permutacją liczb 0..n-1;
pomoce: permut losowe do zadań o LE, synch, O(n) kom

ZADANIE 14 (3pkt) "LE, synch, cykl, uniform, O(n) kom"
Zaimplementuj powyższy algorytm;
użyj symulatora synch (nic dziwnego);